1941. Parent
Write a program
that determines whether one of two given vertices in a tree is a parent of the
other.
Input. The first line
contains one integer n (1
≤ n ≤ 105) –
the number of vertices in the tree.
The second line
contains n integers, where the i-th number represents the parent
of the vertex numbered i. If the value is zero, the vertex is the root
of the tree.
The third line
contains an integer m (1 ≤ m
≤ 105) – the number of queries.
Each of the
following m lines contains two distinct integers a and b (1 ≤ a, b ≤ n), representing a query.
Output. For each of the m
queries, print 1 in a separate line if vertex a is a parent of vertex b,
and 0 otherwise.
|
Sample
input |
Sample
output |
60 1 1 2 3 354 11 43 62 6
6 5 |
0 1 1 0 0 |
SOLUTION
graphs – depth first
search
Algorithm analysis
Let’s represent the
tree as a directed graph, where edges are directed from ancestors to
descendants (to save memory).
Perform a
depth-first search on this graph and assign two timestamps to each vertex v:
·
d[v] – the entry time (when DFS first visits the vertex).
·
f[v] – the exit time (when DFS finishes processing the vertex).
A vertex a
is a parent of vertex b
if the following inequality holds:
d[a] < d[b] < f[b] < f[a]
This means that the
interval [d[b]; f[b]] is fully contained
within the interval [d[a]; f[a]]. Since the inequality d[b]
< f[b] always holds for any vertex b,
checking whether a is a parent of b reduces to verifying two
conditions:
d[a] < d[b] и f[b] < f[a]
Example
The graph from the example, with assigned timestamps,
is as follows:
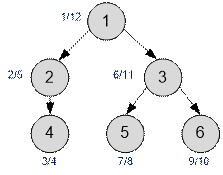
For example, vertex 1 is a parent of vertex 5 because the
following conditions hold:
d[1] < d[5] and f[5] < f[1]
Indeed, the interval [7; 8] is fully contained
within the interval [1; 12].
Algorithm implementation
Since the number
of vertices in the graph can be large, store it as an adjacency list g.
To keep track of
visited vertices, use the used array.
The entry and
exit timestamps for each vertex will be stored in the d and f
arrays, respectively.
vector<vector<int> > g;
vector<int> used, d, f;
The dfs function performs a depth-first search starting from vertex v, assigning the timestamps d[v] and f[v].
void dfs(int v)
{
used[v] = 1;
d[v] = time++;
for (int to : g[v])
if (!used[to]) dfs(to);
f[v] = time++;
}
Функция is_Parent возвращает 1,
если вершина a является предком вершины b, и 0 в противном случае. Для этого проверяется включение
отрезка [d[b]; f[b]] в отрезок [d[a]; f[a]], что
эквивалентно выполнению двух неравенств:
d[a] < d[b] и f[b] < f[a]
int is_Parent(int
a, int b)
{
return (d[a]
< d[b]) && (f[b] < f[a]);
}
Основная часть
программы. Читаем количество
вершин графа n.
scanf("%d",&n);
Инициализируем массивы.
g.resize(n+1);
used.resize(n+1);
d.resize(n+1);
f.resize(n+1);
Читаем входной
граф. Если вершина a является
родителем вершины i, добавляем в граф
ориентированное ребро (a, i) (для экономии памяти используем представление в
виде ориентированного графа). Вершины графа нумеруются числами от 1 до n. Если a = 0, то вершина i
является корнем дерева, и в этом случае ребро не добавляется. В переменной root находим номер вершины,
являющейся корнем.
for(i = 1; i <= n; i++)
{
scanf("%d",&a);
if(!a) root =
i; else g[a].push_back(i);
}
Запускаем поиск в глубину из корня root.
dfs(root);
Читаем запросы и выводим ответ на
каждый из них за константное время.
scanf("%d",&m);
for(i = 0; i < m; i++)
{
scanf("%d
%d",&a,&b);
printf("%d\n",is_Parent(a,b));
}